數理統計學是資料分析的基礎理論，我們之前所有為資料分析所做的工作，比如梳理指標、篩選資料、視覺化等等，都是為了我們能夠更好地找到資料之間的關係，利用統計學原理對這些關係進行界定和聯繫。
但是在實際分析中，我們很可能會因為沒有避開數理統計中常見的【踩雷】，造成我們最終分析結果與實際偏差很大， 我主要總結了三個方面：

• 錯把數理關係當成因果關係
• 不同變數之間會存在悖論
• 資料統計有偏差

一、不要把資料統計關係當成因果關係

我們先看三個例子：

1、彩票悖論

首先根據假設檢驗，如果原假設概率非常小，就可以拒絕原假設。假設0.0001就是一個非常小的概率，組織一次公正的10000張彩票抽獎活動，按照之前的假設，1號彩票中獎的概率是0.0001，是要拒絕的，依次類推，我們可以拒絕所有的彩票，那麼就沒有彩票可中獎，但現實情況是總會有中獎的彩票，這是統計和邏輯不相符的一個例子。

2、無票入場者悖論

假設在一個有1000個座位的音樂廳舉辦一場音樂會，主辦單位只售出了499張票，但當音樂會開始的時候，1000個坐席卻都坐滿了，這時主辦單位有權向每個人收票錢，因為每個人無票入場的概率都是50.1%，這樣音樂廳雖然只有1000個座位，卻將會有1499張門票的收入，但實際情況並非如此。

3、生日悖論

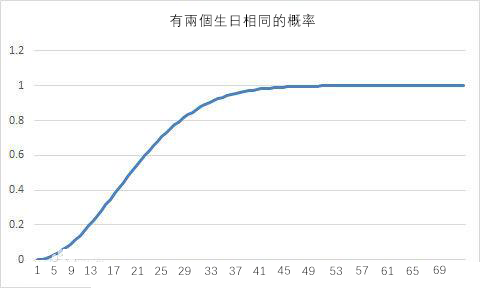
先來看一個問題：如果一個班裡有23個同學，那麼他們當中至少有兩個人生日相同的概率是多少？
按照常識我們會覺得這個概率應該挺小的，畢竟一年365天，23個人撞期，還是挺小的，然而結果卻是50%，也就是說有50%的概率這23個人中有兩個人生日相同。

這裡的50%到底是什麼意思呢，是說只要是一個班裡有23個及以上的學生，就一定有一半的概率兩個人同一天生日嗎？

請回看我們這一節的標題：統計關係並不等於因果關係，這句話很重要，理解它更重要。
上面3個例子說明了以概率為依據做決策是不合邏輯的，然而邏輯和統計本身卻是大不相同，在邏輯上，一個命題只有對和錯兩種劃分，而在統計上，卻可以說成對的概率有50%，錯的概率為20%，就是這一點不確定性造就了以邏輯推理和統計為基礎所得決策上的不一致，或者說矛盾，這就是統計關係不等於因果關係。
在進行資料分析的時候，我們尤其要注意這個坑：比如當我們的資料顯示肺癌的人80%都是因為抽煙時，我們就不能說所有抽煙的人都會導致肺癌。

二、變數關係存在的兩個悖論

1、辛普森悖論

指當我們對兩個變數進行分組研究時，在分組中都佔優勢的一方，在總評中反而成為失勢的一方。

比較著名的當屬1973年加利福尼亞大學伯克利分校性別歧視的例子，男生錄取率為44%，女生錄取率為35%，根據這個資料有人就覺得該校有性別歧視的傾向，但如果每個院系分開來看錄取率的話，可以發現，A B D F四個院女生的錄取率都高於男生。這個悖論告訴我們一個簡單的統計數字不能完全描述其背後的複雜意義，和我們平時熟知的描述性統計分析有點矛盾哦，可以好好思索一下。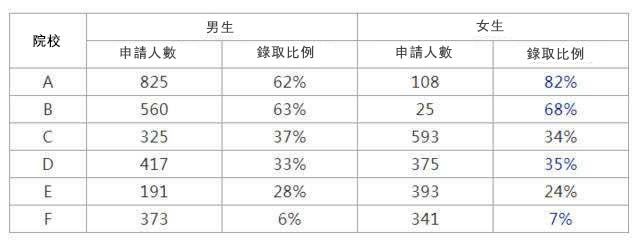

2、伯克森悖論

伯克森悖論，指的是兩個本來無關的變數之間體現出貌似強烈的相關關係。
如假設某學生的文化成績高那麼他的體育成績就不好，體育越好，文化成績就越差，這好像也成為了我們平時的一個認知，班上的尖子生好像體育成績都不怎麼好，這種現象是怎麼出現的呢？
假設學生要參加兩種類型的考試，即文化和體育課，其中任何一種類型的考試達90分以上就可以畢業，那麼畢業的學生要麼在文化考試中考到90分以上，或者在體育考試中考到90分以上，或者在兩門考試中都考到90分以上。通常情況下正常人只需要選擇一種類型的考試努力發揮到極致就好了，另一個沒關係對吧，因此會呈現出學生的文化成績和體育成績是負相關的關係。
伯克森悖論還可以用來解釋為什麼很多人都存在帥哥都是渣男的印象，還有顏值超高的小鮮肉演員演技不忍直視，這些現象。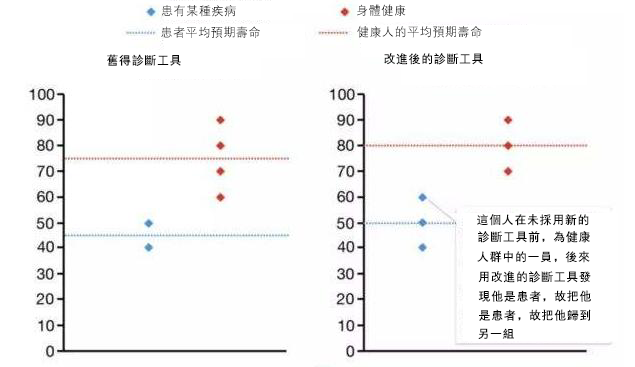

三、統計偏差造成資料分析失誤

1、賭徒謬論

賭徒謬論是指，相信一個結果已經發生了，那麼再發生的機會就會很低。
比如一個賭徒在打賭硬幣是正面朝上或是背面朝上時的情景，前面5次的結果都是正面朝上，那麼下一次他覺得反面朝上的概率會更大，這就是賭徒謬論。為什麼說是謬論呢？因為高中的時候我們就學過扔硬幣這個問題的概率，每扔一次一枚硬幣是一個獨立的事件，正面朝上和反面朝上的概率相同都是0.5，不受前面扔了多少次的影響，也就是說雖然前面5次都是正常朝上，下一次仍是正面朝上的概率也還是0.5。
聊到這，可能有些人會不理解了，或者腦海裡依稀記得好像老師講過，扔一枚硬幣扔個1000次，正面朝上和反面朝上的次數都是接近一半的呀，能想到這裡的同學，恭喜你，已經入門了。
確實如此，但請看清楚前提：扔1000次，這就是大數定理，當我們大量重複某一相同實驗時，最後的結果會穩定在某一數值附近，但把大量重複事件的規律運用在少數的事情上就錯了。

2、倖存者偏差

指的是只能看到經過某種篩選而產生的結果，忽略了被篩選掉的關鍵資訊。
在二戰期間，人們發現倖存的轟炸機中，機翼中彈的數量很多，而機身中彈的卻很少。因此人們認為我們應該加固飛機的機翼，其實不然，就是因為機翼中彈多還能飛回來，所以機翼中彈並沒有影響飛機返航；而機身中彈的少則說明了子彈打中機身對飛機的影響更大，導致飛機不能返航，在這個飛機問題中，只統計到了倖存下來的飛機，以此下結論，是不正確的。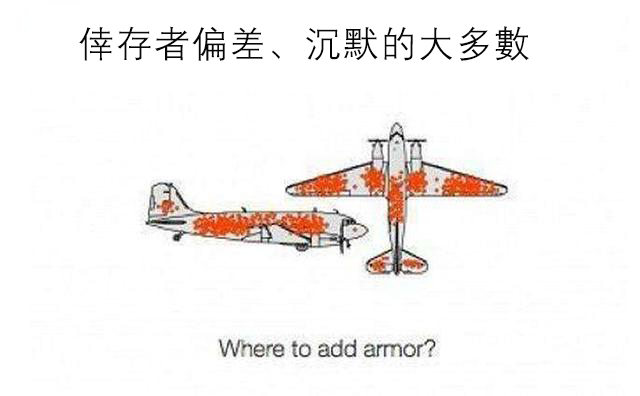

現實生活中也有很多倖存者偏差的案例，比如在仰慕商業巨頭的時代里，很多人盯著商業大佬的成功路徑，并對他們的商業思維競相模仿。從結果來說，能複製一個商業帝國的可能性微乎其微，因為他們很多是在複雜環境中的倖存者而已，並且大多時候大佬們會有意無意抹去僥倖的那些部分。所以，聽他們避雷、填雷、挖雷，比學習他們的成功經驗更有效喔。
今天就分享到這。

我是「數據分析那些事」。常年分享數據分析乾貨，不定期分享好用的職場技能工具。按贊我的臉書，期待你與我的互動！